A function for which fxy ≠ fyx
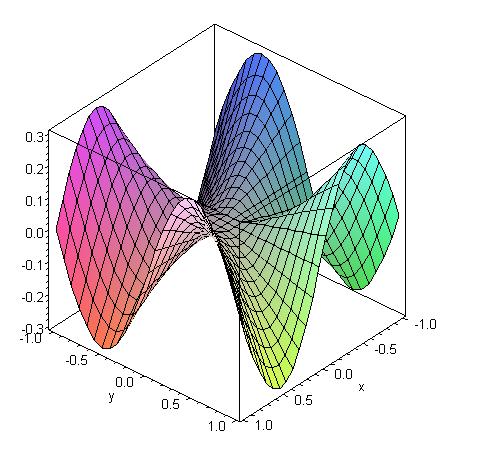 |
| Graph of the function given by f(x,y) =
(x3y - xy3)/(x2 + y2)
for (x,y) ≠ (0,0) and f(0,0) = 0. |
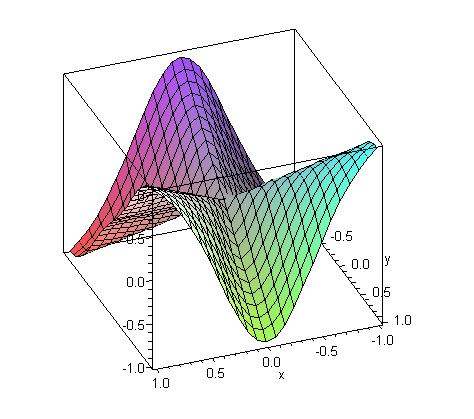 |
| Graph of fx. Note that the slope in the y-direction
through the center of the graph appears to be negative. It can indeed be verified that fxy(0,0) = -1. |
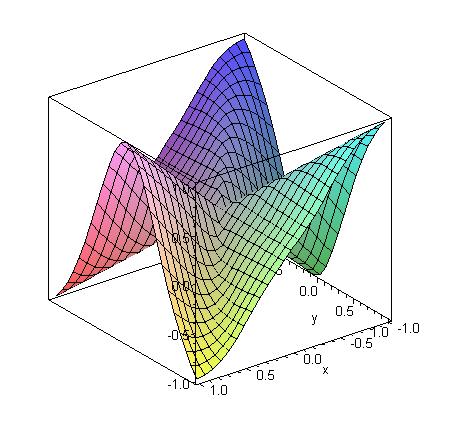 |
| Graph of fy. Now note that the slope in the x-direction
through the center of the graph appears to be positive. In this case one finds that fyx(0,0) = 1. |
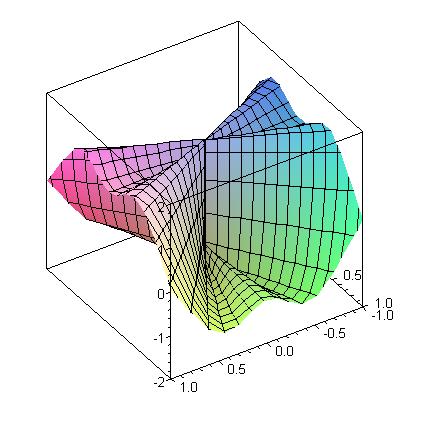 |
| For (x,y) ≠ (0,0), Clairaut's Theorem guarantees that fxy = fyx, the graph of which is shown here. The "pinch" in the center of the graph explains why Clairaut's Theorem does not hold at (0,0). |