Parametric Curves
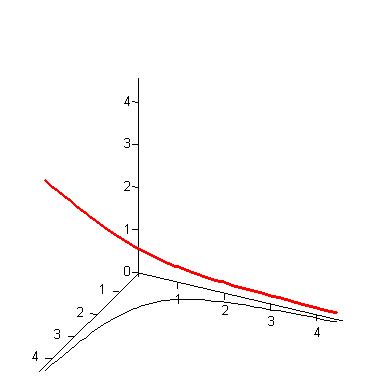 |
| A graph of the curve (in red) with vector equation
r(t) = <et,
e-t, et>. The black curve is its projection onto the xy-plane. |
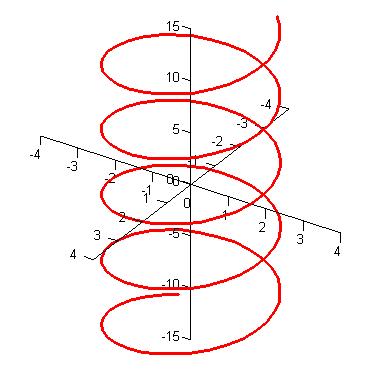 |
| The curve r(t) = <2cos(t), 2sin(t), t>. |
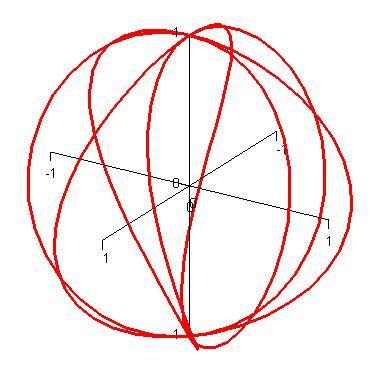 |
| The curve r(t) = <cos(t) sin(4t), sin(t) sin(4t), cos(4t)>. |
 | 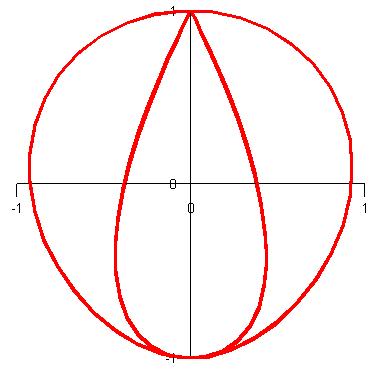 | |
| The projections of r(t) = <cos(t) sin(4t), sin(t) sin(4t), cos(4t)> onto the xy-plane (left) and the yz-plane (right). | ||
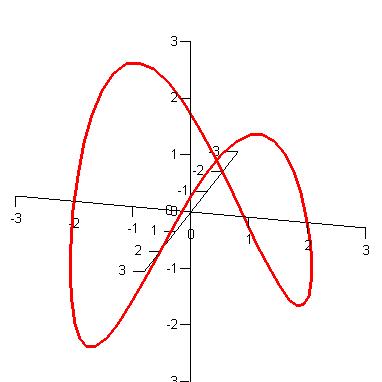 |
| The curve r(t) = <2cos(t),2sin(t), 2sin(2t)>. |
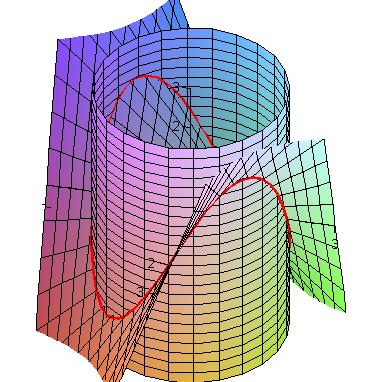 |
| The curve r(t) = <2cos(t),2sin(t),
2sin(2t)> and the surfaces x2 + y2 = 4, z = xy. |